Electronics

What kind of load is an incandescent bulb?

On electronics.stackexchange  user T.S., PhD and whatever, and a notorious troll (whose account at one time was suspended for nearly 3 years) tried to challenge me claiming an incandescent bulb is not a resistive load. His argument was that the resistance isn't linear. So my reply to T.S. (for a while, until he became rather obnoxious) was: if it's not resistive, then what is it?

Types of loads

There are 3 kinds of electric loads: capacitive, inductive, and resistive.

1. Inductive loads

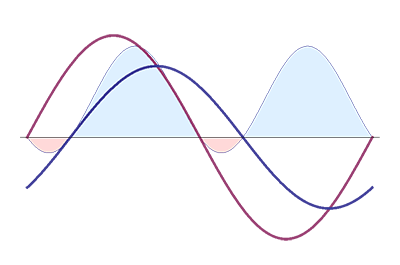
The figure at the left shows how voltage and current relate under an inductive load. When you apply a sine voltage (purple curve) the current (blue curve) won't be exactly in phase, but come slightly later. That's because the current has to build up a magnetic field, and magnetic fields are very conservative: they will resist changes to the field.
This phase shift has an important consequence: there will be some time when voltage and current won't have the same sign. The voltage will go negative while the current is still positive. Now, since power = voltage x current, power will be negative at that moment. That's shown in the graph in the power curve (the color-filled one). This means that the inductor won't take power (the light blue area), but will release power (the light red area). The inductor becomes a power source.

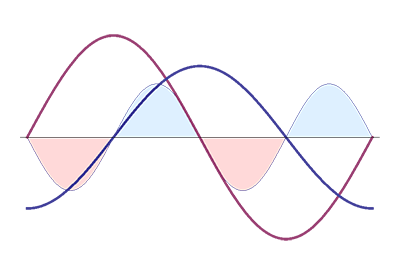
Where does this power come from? It comes from the magnetic field built up earlier. Magnetic fields can store energy. Notice that the blue area is larger than the red one. This means that the released power is less than the absorbed power. The difference is lost in the form of heat in the coil's resistance.
When we have a look at an ideal inductor, without any resistance, we'll see that the phase shift becomes 90° and the red area becomes the same size as the blue one: all the absorbed power is released again.

2. Capacitive loads

A capacitor is the dual of the inductor. The same story goes, but with voltage and current trading places. Applying current will build up a voltage on the capacitor, but just like the inductor's current doesn't follow the voltage immediately, for the capacitor it's the voltage which lags the current.

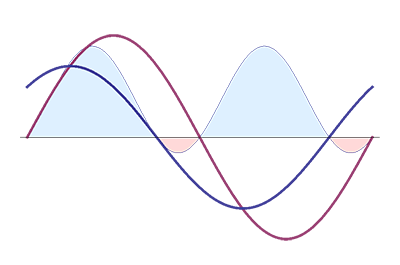
Here also we have a situation where during a part of the cycle voltage and current have opposite signs, and power is negative. All in all, the graph at the left is very similar to that of the inductor. So also in the case of the capacitor energy is re-released. Unlike the inductor the capacitor stores the energy in an electric field. Because the phase shift in the graph is again less than 90° there will be power lost in the capacitor. An ideal capacitor will have a 90° phase shift, and the absorbed power will be the same as the released power. Neither ideal capacitors, nor ideal inductors consume any power.

3. Resistive loads

We saw that for inductive loads current trails voltage, and for capacitive loads voltage trails current.

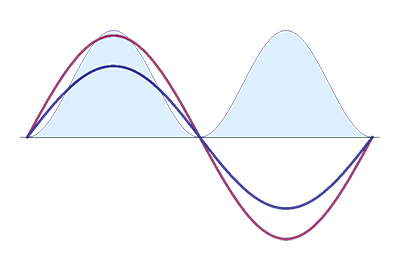
The third situation is then when voltage and current are in phase with each other, shown in the last graph. Since there's no phase shift voltage and current always have the same sign, and power is always positive. There's no energy stored in either magnetic fields or electric fields, and no energy re-released. This is the purely resistive load, and the consumed power is converted into heat and radiation.

Back to the bulb

The photo shows clearly that the filament is coiled. Isn't that an inductor then? Well, let's see. The inductance of a one layer coil is determined as $$ L (\mu H) = \dfrac{radius^2 \times turns^2}{25.4 (9 \times radius + 10 \times length)} $$ with radius and length in millimeters. If we estimate for a 230V/60W bulb a radius of 1mm, length 25mm and 100 turns we get $$ L = \dfrac{0.5^2 \times 100^2}{25.4 (9 \times 0.5 + 10 \times 25)} = 390 nH $$ The impedance of this bulb is $$ Z = \dfrac{V^2}{P} = \dfrac{(230V)^2}{60W} = 880\Omega $$ Then $$ sin(\phi) = \dfrac{\omega L}{Z} = \dfrac{2\pi \times 50Hz \times 390nH}{880\Omega} = 1.4 \times 10^{-7} $$ and $$ cos(\phi) = 0.9999999999999905 $$ aka "1".

Conclusion

Compared to its resistance the inductance of a bulb is negligible. A bulb doesn't store energy magnetically, nor electrically. A bulb is a resistive load. QED.