Indiana pi

Introduction

We all learned in high school that $\pi$ is an irrational number, i.e. you can't represent $\pi$ as a fraction. In practice, however, we often use simple fractions to approximate $\pi$. We'd say $\pi$ = 3.14, which is equivalent to the fraction $\frac{314}{100}$, or we'd use $\frac{22}{7}$, which is a slightly better approximation. When I was in high school I serendipitously discovered the fraction $\frac{355}{113}$, which approximates $\pi$ to 6 decimal digits. I was pretty proud of my discovery, until I learned that it had already been known by the Chinese in the 5th century.
Furthermore $\pi$ is also transcendental, which means it's not the root of any polynomial equation with integer coefficients. A polynomial equation is of the form $$a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x^1 + a_0 = 0$$ For instance, the irrational number $\sqrt{2}$ is not transcendental because it's a root of $$x^2 - 2 = 0$$ When Johann Heinrich Lambert proved in 1761 that $\pi$ is irrational, he conjectured it might be transcendental. This was finally proven more than a century later by Ferdinand von Lindemann in 1882.

Squaring the circle

For centuries mathematicians have been looking in vain for a way to square the circle. This means, starting from a circle $\pi$ square units in area, using only compass and straightedge, construct from that circle a square also $\pi$ square units in area. Lindemann's proof of $\pi$'s transcendence settled the issue once and for all by proving squaring the circle is impossible.

Despite Lindemann's proof some people, often amateur mathematicians, would continue to look for a way to square the circle. This may be called stubbornness, but maybe they didn't have access to mathematical journals and hadn't heard of the proof. One person who kept trying was the amateur mathematician Edward (sometimes referred to as Edwin) Goodwin, who was a physician in the Indiana town of Solitude at the end of the 19th century.
Goodwin didn't have the excuse of not having access to mathematical journals, since he had already published a few articles in the American Mathematical Monthly. I will come back to those later.
Anyway, Goodwin should have known better than publishing a proof for squaring the circle in the American Mathematical Monthly in 1894.

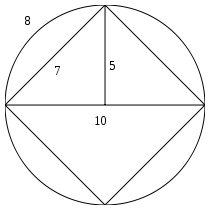
Goodwin's “circle” is shown at the right. I put the word “circle” in quotes because even at first glance it doesn't look like a circle: at the top, left, right and bottom the four segments don't connect smoothly. Also, Goodwin manages to have 4 segments of 8 units long, giving a circumference of 32 units. His diameter is 10 units long, giving a value for $\pi$ of $\frac{32}{10}$, or 3.2.

That was Goodwin's “invention”: a value for $\pi$ of 3.2, instead of the “wrong” (sic) value of 3.1415926…

(Also note that in Goodwin's construction the square root of 2 is $\frac{7}{5}$ or 1.4, even though it had been known since antiquity that $\sqrt{2}$, 1.4142…, is irrational.)

The bill

Goodwin also thought he could make money from his invention: people would have to pay royalties for using 3.2 as a value for $\pi$, except for the citizens of Indiana, for whom its use would be free. To this purpose he proposed a bill to Indiana Representative Taylor I. Record, which the latter introduced in the House under the long title:

“A bill for an act introducing a new mathematical truth and offered as a contribution to education to be used only by the State of Indiana free of cost by paying any royalties whatever on the same, provided it is accepted and adopted by the official action of the Legislature of 1897”.

There was some alarm and disbelief in the press, but generally the press, especially in Indiana, was enthousiastic. That the Indianapolis Sentinel referred to Dr. Goodwin as a mathematician of note was bad, but the Indianapolis Journal really laid it on thick:

“It may not be the function of a Legislature to endorse such discoveries, but the average editor will not gain much by trying to make fun of a discovery that has been endorsed by the American Mathematical Journal; approved by the professors of the National Astronomical Observatory of Washington, including Professor Hall, who discovered the moons of Mars; declared absolutely perfect by professors at Ann Arbor and Johns Hopkins Universities; and copyrighted as original in seven countries of Europe. The average editor is hardly well enough versed in high mathematics to attempt to down such an array of authorities as that. Dr. Goodwin's discovery is as genuine as that of Newton or Galileo, and it will endure, whether the Legislature endorses it or not.”

It is hard to believe that those professors actually endorsed Goodwin's ridiculous ideas. He may have written to them, received no rejection (because they thought it was too ridiculous to reply) and seen this as an endorsement. It's also very well possible that the egotistic Goodwin wrote the article himself. Indeed, which editor would compare Goodwin to Newton, the greatest scientist of all times, if he didn't understand the “high” (sic) mathematics himself?

Bill 246 passed unanimously in the full House of Representatives on 5th February, 1897. One can safely assume that a number of Representatives hadn't even read it.

Professor Waldo

Enter Prof. Clarence Waldo. Professor Waldo was the head mathematics professor at Purdue University at the time, and was visiting the Statehouse regarding the university's budget appropriation. When he heard that the General Assembly was debating mathematical legislation, he, of course, listened in, astonished. He could hear an ex-teacher say: “The case is perfectly simple. If we pass this bill which establishes a new and correct value of $\pi$, the author offers our state without cost the use of this discovery and its free publication in our school textbooks, while everyone else must pay him a royalty.”.
When after the debate a Representative offered to introduce him to Dr. Goodwin, Professor Waldo replied that he was already acquainted with as many crazy people as he cared to know.

Waldo realized he had to step in, and he started to coach the Senators about the ridiculous bill. As a result the bill got a completely different reception than had been the case in the House of Representatives. The Indianapolis News reported on 13th February

“…the bill was brought up and made fun of. The Senators made bad puns about it, ridiculed it and laughed over it. The fun lasted half an hour. Senator Hubbell said that it was not meet for the Senate, which was costing the State $250 a day, to waste its time in such frivolity. He said that in reading the leading newspapers of Chicago and the East, he found that the Indiana State Legislature had laid itself open to ridicule by the action already taken on the bill. He thought consideration of such a propostion was not dignified or worthy of the Senate. He moved the indefinite postponement of the bill, and the motion carried.”

And that's still the current state of bill 246.

Who is to blame?

It looks like the Representatives are to blame, for not understanding mathematical truths are not created by law. However, the bill's series of mathematical claims was followed by a recitation of Goodwin's previous accomplishments:

“…his solutions of the trisection of the angle, doubling the cube and quadrature of the circle having been already accepted as contributions to science by the American Mathematical Monthly … And be it remembered that these noted problems had been long since given up by scientific bodies as unsolvable mysteries and above man's ability to comprehend.”

So it looks like the Representatives, many of whom admitted that they didn't have the knowledge to understand the bill completely, relied on the authority of the American Mathematical Monthly. After all, Goodwin had published solutions for three mathematical problems, which were known to be impossible. The blame is on AMM! They added a disclaimer that Goodwin's contributions were published at the author's request, but his papers should never have been published at all, despite the disclaimer. You don't publish articles which you know are rubbish under no circumstances. All three: trisection of the angle, doubling the cube, and squaring the circle had been proven to be impossible, and anyone claiming he found a proof of the possibility after all should be treated the way he is: an idiot.

What could have happened?

One may wonder what would have happened if the bill was passed in the Indiana Senate as well. Probably not much. Nobody outside of Indiana was going to pay royalties for something that was obviously completely wrong, and even in Indiana common sense would prevail over thriftiness. The one or two businesses who would calculate their circumferences as 3.2 times the diameter soon would have to retrace their steps or go out of business. Everybody else would simply ignore the bill, and the number 3.2. Goodwin wouldn't have made a penny of it.

Goodwin

Goodwin was called an amateur mathematician, but I think that's too much praise. It's clear that he didn't have the slightest understanding of mathematics, but was encouraged in his fool's errand by the acceptation of his writing by a mathematical journal. All in all Goodwin was an idiot and a kook, much more than the State Representatives were, and any peer-review process should have exposed him.

So this court finds Edwin Goodwin guilty of trying to overthrow established and proven mathematics, but we plea in extenuation that in his ridiculous attempt he gave us a good laugh.

Indiana House Bill No. 246, 1897